FROM Triply periodic minimal surface TO ARCHITECTURE
This project will discuss the possibilities of applying Triply periodic minimal surface to architecture design in order to create a highly replicable yet innovative architecture. In order to do that, firstly we choose six minimal surfaces prototypes which have the greatest architectural potential, and then we use computer-aided program (Rhino) to build the model of the proximity of several minimal surfaces from the basic patch to the unit cell and then to the final complex. By decomposing the minimal surface we get the better understanding of the how the complex are formed and symmetry character of each surface. Three feasible ways of building physical model of minimal surfaces are also experimented and explained. And then we examine the spatial quality that is formed by the surface, how topologically the minimal surface changed the spatial logic and how the porosity changes the connectivity and flowability inside of the space. Based on this research, we proposed a design project that applies and reflects the character of the triply periodic minimal surface.
DIAGRAMS AND ANALYSIS
ARC 505
TEAM MEMBER : JEFF BARR
intreduction
A minimal surface is a surface that is locally area minimizing, that is a small piece has the smallest possible area for spanning the boundary of that piece. Minimal surface also has zero mean curvature, which means the sum of principle curvatures at each point is zero (see Fig 1.0). The shape taken by soap bubble is minimal surface (see Fig 2.0). The catenoid, the surface of revolution of a catenary, is a simple example. Since 19th century when the bubble experiment was executed by a Belgium Physicist J. Plateau, more and more researches about minimal surfaces has been done by mathematicians and numerous type of surface has been discovered. Among this minimal surfaces there is one type which is extremely fascinating, that is triply periodic minimal surfaces (TPMS) (no self-intersection). A TPMS can repeat themselves in three dimensions by rotating, mirroring and replicating. It is infinitely extending, has one of the crystallographic space groups as its symmetry group and it partitions space into two labyrinthine regions.
Fig. 1.0- Minimal surface curvature planes
Fig. 2.0- Soap film, Catenoid
The triply periodic minimal surfaces have a great potential for architecture. How to make architecture to be highly moduliable and replicable is always a main concern for architects. In classical times, when we consider that problem, the five Platonic solids (the cube, octahedron, tetrahedron, icosahedron and dodecahedron), along with the sphere, is the fundamental elements and prototype. However, does high modulization equals stereotype and can innovative design come out of high modulization? Is there a prototype which allows for simple replication yet being innovative in form?
When you consider the answer for this question, then Triply periodic minimal surface certainly comes to your mind. First of all, it has numerous variations to accommodate different architectural functions. Secondly, the space that is formed is constantly continuous, and the splendid horizontal parallel space is available. It starts from a simple patch which is controlled by the five Platonic solids, by rotating and repeating, it could form an extremely complex shape.
This project will discuss the possibilities of applying Triply periodic minimal surface to architecture design in order to create a highly replicable yet innovative architecture. In order to do that, firstly we choose six minimal surfaces prototypes which have the greatest architectural potential, and then we use computer-aided program (Rhino) to build the model of the proximity of several minimal surfaces from the basic patch to the unit cell and then to the final complex. By decomposing the minimal surface we get the better understanding of the how the complex are formed and symmetry character of each surface. Three feasible ways of building physical model of minimal surfaces are also experimented and explained. And then we examine the spatial quality that is formed by the surface, how topologically the minimal surface changed the spatial logic and how the porosity changes the connectivity and flowability inside of the space. Based on this research, we proposed a design project that applies and reflects the character of the triply periodic minimal surface.
Fundamental Unit and Surface Patches
One important character about minimal surface is that it has separable properties, meaning: any sub-patch, no matter how small of area, cut from a minimal surface it still has the least amount of area of all surface sub-patches with the same boundary. Triply periodic minimal surfaces is formed by a fundamental unit copying or mirroring itself three dimensionally. The fundamental unit always share a face or part of the face with the unit that is immediately surround it. And the fundamental unit can furthermore be subdivided into surface patch, which is also called an “asymmetric unit”. The surface patch is always controlled by a polyhedron. When it is copied by applying the transformations, it produces a tiling of the space and then forms the fundamental unit.
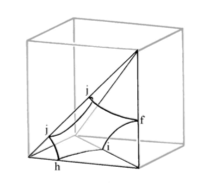
The minimal surface can be specified by the surface patch and the symmetry. Since every minimal surface is unique in surface patch and symmetry, this is what differential the types of minimal surfaces. Figure 4 shows the surface patch and symmetry for Schoen’s OCTO surface. The surface is produced by a surface patch which is a curvilinear pentagon fihjj mirroring along the four faces of the tetrahedron inside of a cube. Since the vertex of the pentagon can be permutated along the edge, it can be morphed into a different shape of Schoen’s OCTO surface. But since the topology and symmetry stays the same we can say these minimal surfaces are topologically equal thus they are the same type.
The various surfaces are extremely difficult to visualize and they can be seen as two levels: the surface patch associated with an asymmetric unit of the space group – the smallest repeating unit, and the complete structure in the cubic unit cell or a rhombic dodecahedron (for a face centered cubic space group) or the 14-faced “Thompson tetrakaidecahedron” which can be repeated to fill all space for the body-centered cubic space group. [1]
Prototype Study
For the following part, we use computer-aided 3d software Rhino to build the approximation models of different minimal surfaces in order to understand the surface patch and the symmetry of each type.
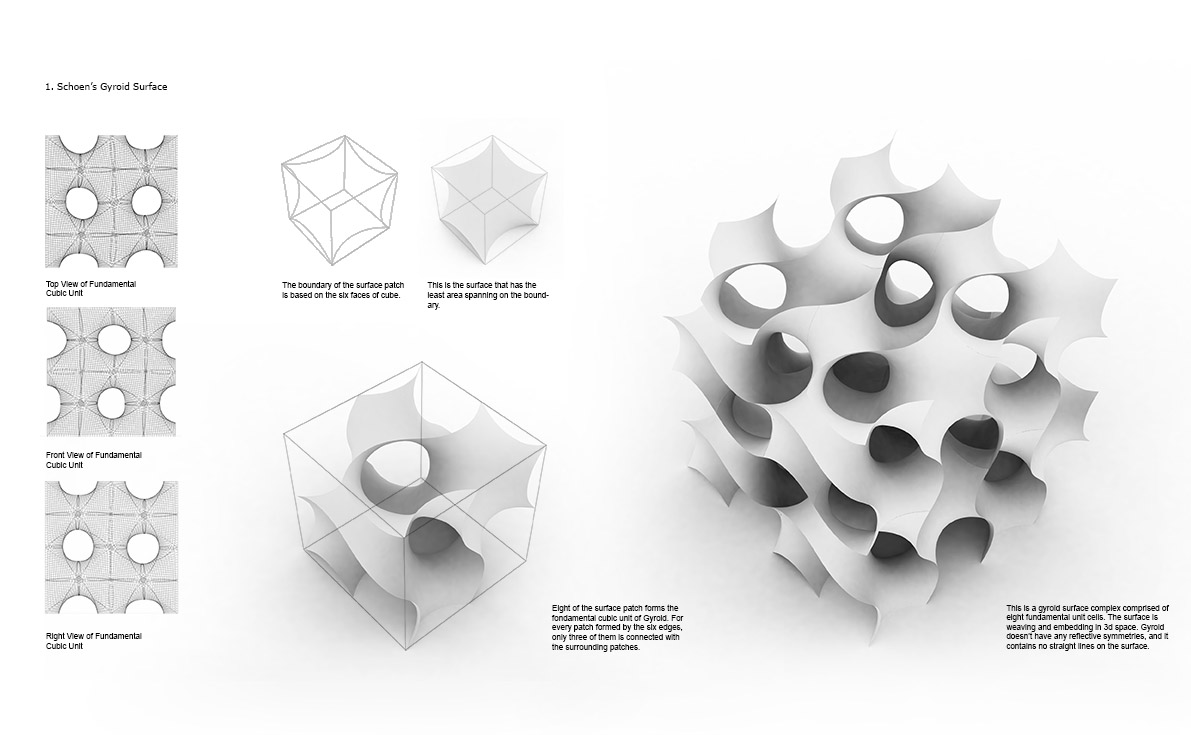
1) Schoen's Gyroid Surface (F.4)
Fig 3.0 show the faces of the cubic on which the six boundary line based. The surface patch, which shows on the third image, is the surface that has the least area spanning on the boundary. Eight of this surface patch then forms a fundamental cubic unit of gyroid, which shows on Fig 4.0. For every patch formed by the six edges, only three of them are connected with the surrounding patches. This gives gyroid surface weaving and embedding in 3d space. One thing that needs to be notice is that gyroid doesn’t have any reflective symmetries, and it contains no straight lines on the surface.
Fig. 4.0- Surface patch and symmetry for Schoen’s OCTO surface
Fig. 3.0 Schoen’s Gyroid Surface
2) Schoen’s Pa (Batwing) Surface (F.5)
The batwing earned is name because of the peculiar shape of the fundamental patch shown outlined on the image. The surface patch fits in the tetrahedron, which is 1/48 the volume of the cubic unit. Then twelve of these patches form the cubic unit cell following the symmetry tetrahedron shown on figure 6. Again, this is only 1/8 of the complete minimal surface lattice cell. There is two ways to assemble the unit cells: to mirror it along the diagonals of the cubic face or to mirror it along the edge of the cube, which makes them look different when assembles together.
Fig. 6.0 - Surface patch and symmetry for Schoen’s Pa
Fig. 5.0 - Schoen’s Pa (Batwing) Surface
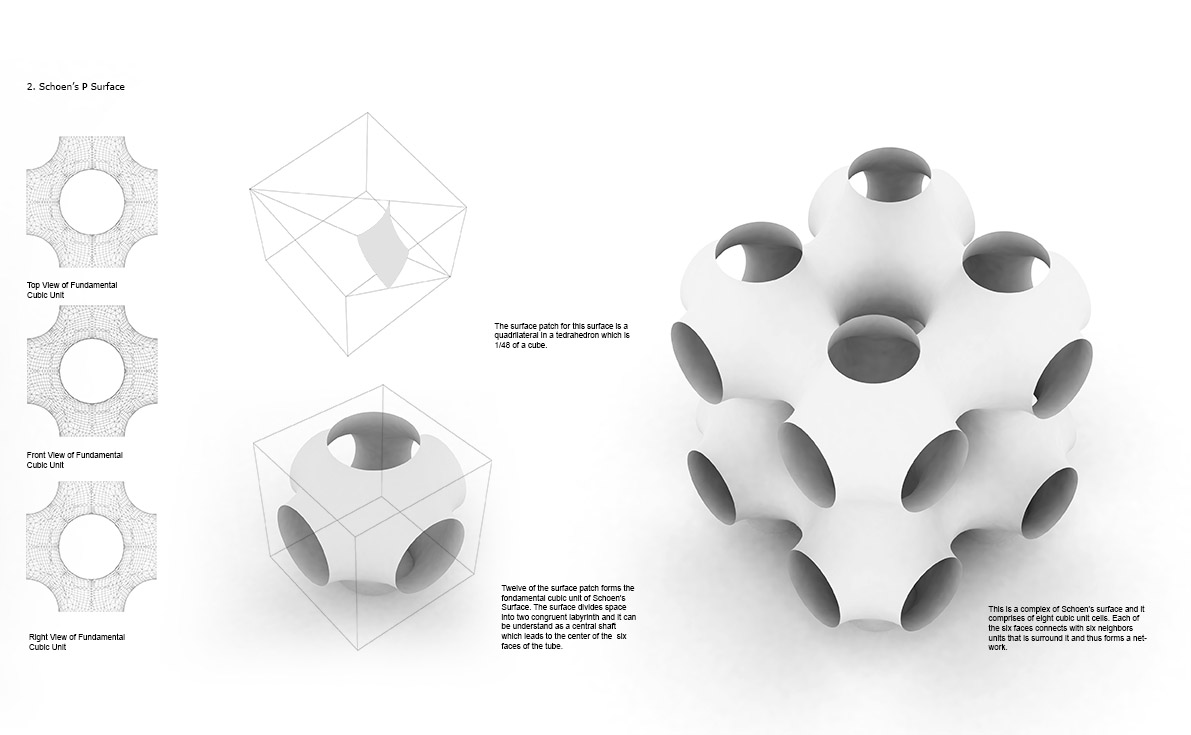
3) Schwatz P Surface (F.7)
The surface patch of this surface, as bounded by mirror planes, is a quadrilateral in a tetrahedron which is 1/48 of a cube, the fourth image shows a cubic unit cell which indicates all embedded symmetry lines. The surface divides space into two congruent labyrinths and it can be understand as a central shaft which leads to the center of the six faces of the cube.
Fig. 8.0 - Surface patch and symmetry for Schoen’s Pa Symmetry
Fig. 7.0 - Schoen’s P Symmetry
4) Schoen’s Manta Surface (F.9)
The simple patch of the Manta Surface is constrained by a tetrahedron which is 1/96 the volume of the cubic unit. 12 of the patch forms 1/8 of the cubic unit and then 8 of the unit forms the cubic unit cell following the tetrahedron symmetry plane the same as shown in Figure 7.
Fig. 9.0 - Schoen’s Manta Surface
5) Minimal Surface on Rhombic Dodecahedron Symmetry
We did one example of rhombic dodecahedron based minimal surface (Fig, 10.0). The logic of forming the minimal surface is the same as the Schwatz P. (Figure 7.0). The difference is: instead of having "the tube openings" on center of six surface of the cube, it has openings on the four diagonal vertex of the rhombic dodecahedron with the angle of 120 degrees in three dimensional space.
Fig. 10.0 - Rhombic Dodecahedron
Physical Modelling Procedure
1) Waffle Structure – Laser Cutter
We try to use waffle structure to build a physical model of the fundamental surface patch of gyroid. The surface is cut by 10 section planes of equal distance in both x and y axis and the section outline then drawn and cut with laser cutter (Fig. 11). The thickness of the material is also taken into consideration when generating the section outline to allow the two intersecting piece to assemble together and form the waffle structure to express the curve surface. (Fig.12)
Fig. 12- Laser Model
Fig. 11- Waffle Structure from Grasshopper
2) Physical Modeling - CNC Carving
The Schwatz P Surface is modelled with plywood on CNC machine. Considering that there is a thickness on the material, we set two volumes for CNC to carve out half of the external side and half of internal side. Finally, we glued the two parts together to make a whole. (Fig.13)
Fig. 13 - CNC Model
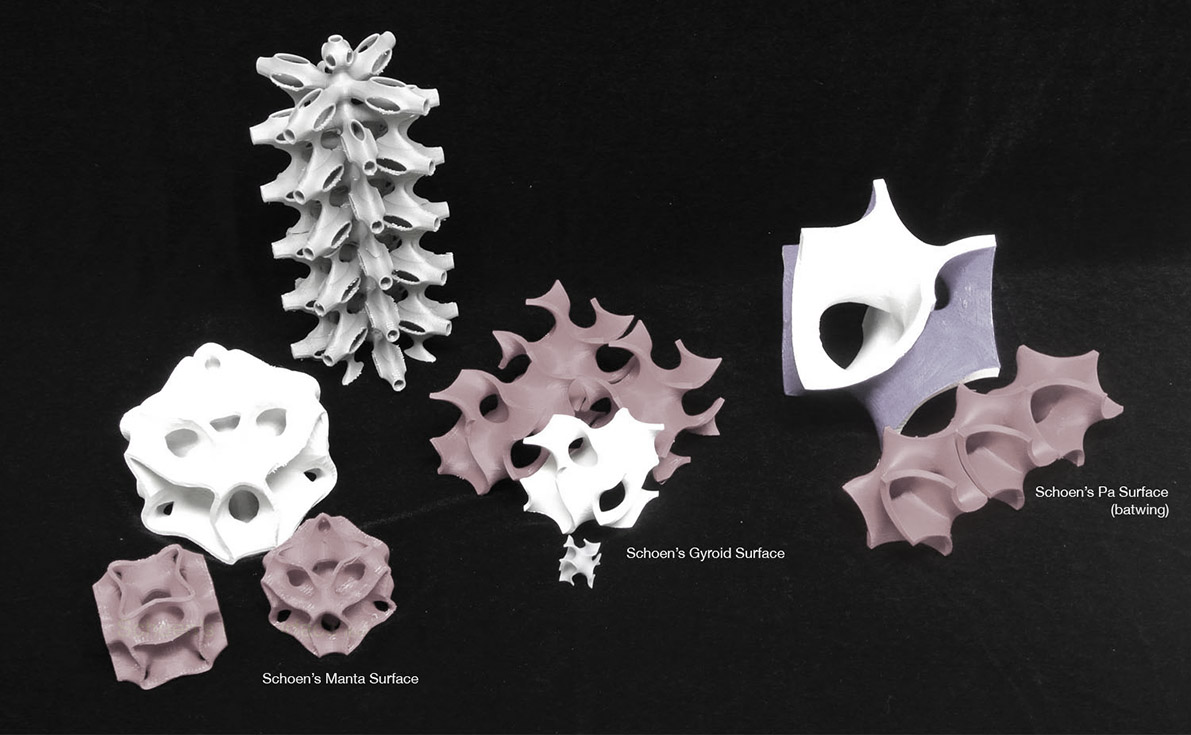
3) Physical Modeling - 3D Printing
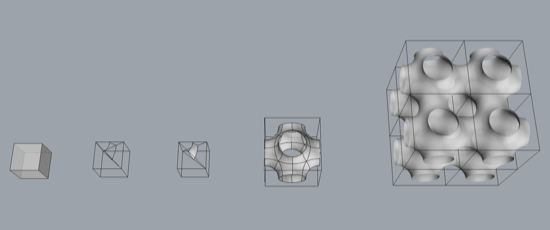
The 3d printing model is done with makerbot’s replicator X2. We save the 3d Rhino model as a stl. file and then sent it to the printer. The model needs to be seamless and one single mesh for the printer to work properly. The printer will analysis where need to have supporting material automatically (mostly happens where there is long cantilever or span). The following image shows three cubic cells printed with 3d printer. (Fig.14, 15, 16)
Fig. 14.0 - Batwing Model
Fig. 15.0 – Gyroid Model
Fig. 16.0 - Manta Model
Spatial Quality Study
Modularity is a feature of triply periodic minimal surface and it has architectural potential for highly repeatable shapes. It can be rearranged and combined to make interesting packing’s. The Manta packing below is example of modular packing. The minimal surface helps to break down the rigid symmetrical surface of typical modular units.
Fig. 17.0 - Manta Packing
Connectivity is another characteristic of minimal and it changes the relationship of one unit with other. Take Schoen’s Manta Surface as an example, each of the six faces connects with six neighboring units (four side, one top and on bottom) that is surround it and thus forms a network. Compared to traditional rigid geometry those connection are on the corners and edges, which does not allow for porosity and Flow-ability.
Porosity is one of the qualities that characterize minimal surface. This porosity allows for a multiplicity of affiliations in the space generated by the minimal surface units and also a higher degree of selective visual connections to occur inside of the space. Figure 19[1] is an example of four unit surfaces from batwing family and we can notice the porosity variations from the evolution of the surface
Fig. 19.0 - Batwing Family.. http://fabiocoletta.blogspot.com/2010/05/porosity.html
Flow-ability of space inside of minimal surface is also an important feature. Since the curvature of every point on minimal surface are zero that means it continuous flows and fill the space. In architectural meaning, it can be understood as that the traditional concept of floor ceiling and wall is vanished and the space is continuously flow from one space to another through a series of weaving surface.
Fig. 20.0 - Manta Sections
Final Application
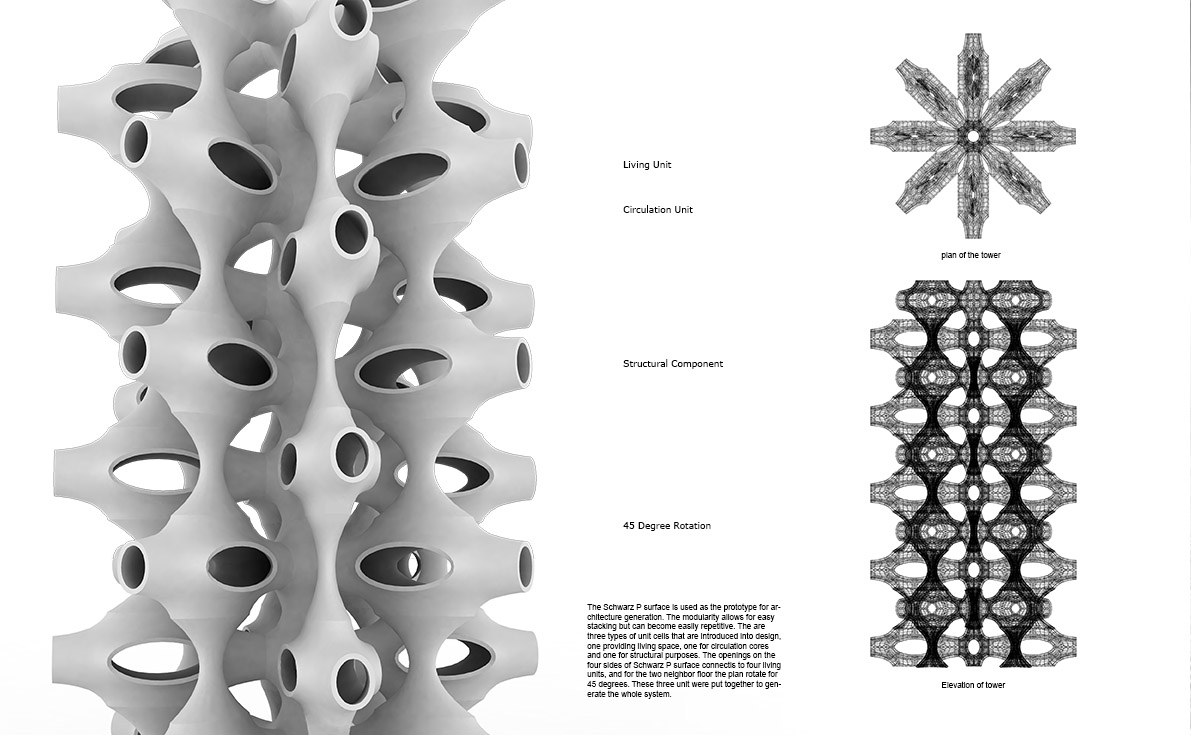
After all our process models we want try applying one of the surfaces to an architectural project. While studying the possibility of aggregation of minimal surface unit based on the spatial characters we choose Schwarz P model. It allowed for maximum internal space. Schwarz P modularity allows for easy stacking but can become easily repetitive. Our proposed design is based on the prototypes of Schwarz P and Catenoid surfaces which take advantage of the modularity characteristics without being monotonous. There are three types of unit cells that are introduced into design, one providing living space, one for circulation cores and one for structural purposes. These three units were put together to generate a whole system. Compared to traditional housing the minimal surfaces porous structure channels circulation, natural ventilation and light.